Additional reporting by Gina Smith for aNewDomain.
aNewDomain — The Italian astrophysicist-artist Aldo Spizzichino died earlier this year, but his memory lives on here at the Heidelberg Laureate Forum (HLF 2017).
The annual gathering of the world’s top computer scientists and mathematicians kicked off here in Heidelberg, Germany today.
A mathematical art exhibit highlighting Schizzichino’s work is for sure an appropriate backdrop at this year’s forum, which unites young researchers with such prize-winning tech and math legends as Internet pioneer Vint Cerf, Google Brain chief Jeff Dean, public key encryption inventors Whitfield Diffie and Martin Hellman, and 20 other innovators who’ve received the ACM AM Turing Award, Fields Medal, Abel Prize, Nevanlinna Prize and the ACM Prize in Computing.
One of the first artists to create mathematical art in computer graphics, Spizzichino began using Fortran 77 and an Apple II in the mid 1970s to explore a litany of mathematical shapes and structures. In subsequent years, he pioneered a number of the techniques you now see in modern graphics software, including ray casting and texturing. Some of his techniques he developed by hand are to this day difficult with even the most cutting edge CG software.
But the main thing Spizzichino offered the world, in the end, was the maths.
Note: To read this story in Dutch, head here.
Through his exploration of Archimidean and Pythagorean surfaces, and of fractals, tesselations, hyperbolic transformations and rotogons (which he conceived), he revealed a world that previously only the mathematically astute could see.
Some of the works on display here at the exhibit, called ‘Math <=> Art’, are deceptively simple. Check out the below Spizzichino image. In it, he is merely depicting the Padovan sequence — 1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 12 … That’s the the little sister of the famous Fibonacci sequence.
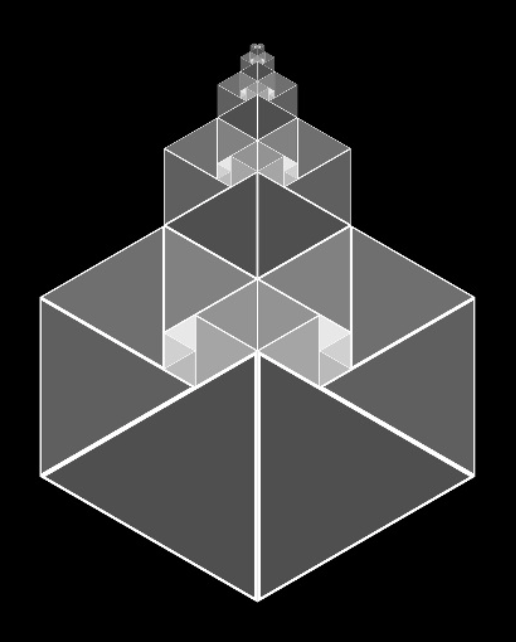
Here’s an image he created that features the golden section spiral.

And here’s my personal favorite: Fall in a Fibred Place. Here, Spizzichino represents an icosidodecahedron such that each face is what one would see if one was looking through the polyhedron from the center of each face, using a fish-eye lens. Notice the background is deformed in a manner similar to how space-time curves around the massive object. Not only is it quite artistic, but it is an accomplishment that proves difficult even with the modern graphics software.
Check it out:

My second favorite is ‘Spaceship of Knowledge’, which depicts a hyperbolic projection of a heptagonal tessellation is shown. These mathematical notions are, admittedly, hard to explain, but they clearly show Spizzichino’s sense of humor. At the same time, it’s easy to see his daytime job embedded in these images. Astrophysics is somehow embodied here.

Another memorable image is ‘Playing Generations’, which represents the so-called ‘horned sphere’ of James Alexander with some intriguing superficial tiling. Because the fractal image shows only two generations, it doesn’t fully express the idea of fractal as such. It’s a poetic title nonetheless.

Spizzichino really knew what a fractal is, of course, which another image, ‘Zigzag path to a fractal island,’ makes clear. Here he combined the Gosper’s Flake fractal by circular inversion to produce a path converging to an island in the middle, which he called ‘Neverland.’ This image doesn’t require that anyone understand all this math to enjoy it, just as you don’t need to have met Peter Pan to enjoy J.M. Barrie’s Peter Pan.

As I was leaving the exhibit, a fellow exhibition-goer by the name of Benjamin Morley made an insightful observation that stuck with me. “I think the artist was using the math to produce interesting things in his art, but I don’t think the art was telling as much about the mathematical objects that we didn’t already know,” he said, adding: “It contrasts for instance with William Thurston’s famous notes on three-dimensional geometry and topology…”
Thurston was an American mathematician and winner of the 1982 Fields Medal, one of the prizes that’s being highlighted here this week at HLF 2017. In his book on 3D geometry and topology, Thurston wrote: “Algebraic geometers like me appreciate how Thurston conveys information through the drawings about what is going on in the geometry, and so in his work the diagrams and the illustrations do tell something about the mathematics. Of course, the algebraists will say that is not satisfactory, but it does strengthen the spatial intuition …”
“And so”, says Morley, ”the title ‘Math <=> Art’ should perhaps not have included a mathematical equivalence sign, but an implication: ‘Math => Art.’“ That bright, tongue-in-cheek observation is one that the technologists and mathematicians here at the Heidelberg Laureate Forum will fully appreciate.
For aNewDomain, I’m Dirk Huylenbrouck.
Here’s a video explaining rotogons, which Spizzichino conceived during his long artistic career. -ED.













